
La física parece incapaz de unificar relatividad y mecánica cuántica. La causa podría ser una insuficiencia en las matemáticas, que evolucionan a lo largo del tiempo pero no sufren revoluciones. Tal vez para seguir profundizando en el conocimiento de la realidad sea necesaria una revolución tan radical que cambie incluso la lógica y las reglas básicas de la razón.
La física en su laberinto
Para un profano la situación actual de la física es bastante curiosa. Hace unos cien años se formularon las dos teorías más importantes de que disponemos hoy: la relatividad y la mecánica cuántica. Describen ámbitos diferentes de la realidad, y ambas supusieron una ruptura espectacular con algunas concepciones básicas de las teorías anteriores. Entre otras, la relatividad rompe con la idea de un tiempo regular y un espacio homogéneo, y la mecánica cuántica rompe con la idea de la continuidad en los procesos físicos. Han pasado cien años y todavía no han sido superadas. Este hecho podría considerarse como un mérito de las propias teorías, o de los físicos que las formularon, o también como un demérito de los físicos posteriores. Pero es que hay un pequeño problema: ambas teorías son incompatibles. ¿Cómo es que no se ha resuelto esta incompatibilidad?
Debe ser incapacidad de los físicos posteriores, entonces. Pero nunca ha habido tantas mentes brillantes investigando, tan bien formadas y con tantos medios. Bueno, pues debe ser que el azar determinó que hace ciento y pico años naciera una generación genial de científicos, y aquella tirada mágica de los dados del azar todavía no se ha repetido. Pero también hay un pequeño problema. Los propios creadores de las teorías en cuestión dedicaron grandes esfuerzos a la unificación de ambas, que les llevaron, en ocasiones, a formulaciones imprudentes de las que luego se arrepintieron.
Es una situación curiosa. Parece que se haya llegado a un límite. Tal vez el universo no es explicable para la mente humana, bien sea por culpa del universo, que no es coherente, bien sea por culpa de la mente humana, que es limitada. Ante esta disyuntiva lo natural es elegir la segunda opción. Por modestia. O por arrogancia, según se mire: estamos tan seguros de que el universo tiene que ser coherente que estamos dispuestos a autoacusarnos antes que a negarlo. ¿Y por qué tiene que ser coherente, el universo? Porque de lo contrario no funcionaría como funciona nuestra propia razón.
La opción de que el universo no sea coherente no es tan grave, a efectos prácticos. La situación que resultaría de ello sería que hay muchos ámbitos de explicación y para cada uno de ellos podemos aspirar a una teoría que lo explique, pero no los podemos reunir todos en uno solo. Lo que sucede en física teórica entre la relatividad, que explica lo muy grande, y la mecánica cuántica, que explica lo muy pequeño, sería lo mismo que sucede entre la bioquímica y la psicología. Ambas explican el comportamiento humano, la bioquímica desde el ámbito de la materia y la psicología desde el ámbito de los procesos mentales o la conducta, pero no es posible conectarlas entre sí. Por ahora. Los neurocientíficos están muy seguros de que algún día conseguirán hacerlo, pero también lo estaba Einstein de que algún día se conseguiría formular una teoría unificada. Y aquí estamos.
Lo malo de esta opción es que cierra un camino de investigación, o especulación, que resulta muy atractivo. Pone límites al conocimiento, y esto cuesta de aceptar. El “ansia de generalidad” es consustancial a la razón humana, como dijo Kant. Por tanto parece más interesante volverse hacia la otra opción y preguntarse: ¿qué nos falla, qué nos falta, de qué carecemos para explicar el universo? ¿No podríamos hacer algo para suplir esta deficiencia?

El agotamiento de las matemáticas
Exploraré tentativamente una posible respuesta a estas preguntas. Por lo menos a la primera: nos fallan las matemáticas. Éstas son el instrumento básico de física. Si el instrumento no da más de sí, poco pueden hacer los pobres investigadores. Pero con esta respuesta parece que regresamos al punto de partida: ¿Por qué no avanzan las matemáticas? ¿Son las propias matemáticas las que no dan más de sí, o son las mentes de las personas que se dedican a ellas?
Hay que reconocer que si la culpa fuera de los matemáticos, absolverlos de su incapacidad sería más fácil que absolver a los físicos de la suya. Al fin y al cabo los matemáticos se dedican a las matemáticas, no a la física. Es evidente que de manera preferente orientan sus investigaciones hacia los ámbitos de mayor demanda, como puede ser la física teórica, pero ellos no son físicos, y no sería justo exigirles que elaboraran el tipo de cálculo necesario para que un físico, al conocerlo, viera en él el instrumento que necesitaba para resolver sus propios problemas.
Lo cierto es que en el pasado los matemáticos han ido suministrando a la física los instrumentos necesarios para que avanzara. En realidad ambas ciencias están tan estrechamente vinculadas que en ocasiones son los propios físicos los que desarrollan el aparato matemático que necesitan, como hizo Newton con el cálculo infinitesimal. Por tanto podría pensarse que el “estancamiento” de la física teórica es consecuencia de un cierto “agotamiento” de las matemáticas.

Ciencia normal y ciencia revolucionaria
Para profundizar en el análisis de esta posibilidad utilizaré el punto de vista de Tomas Kuhn sobre la historia de la ciencia, concretado en su idea de que la ciencia avanza mediante revoluciones. Cuando fue formulado a finales del siglo pasado este punto de vista rompía con la concepción tradicional de que el avance científico se produce más bien por acumulación continua: los científicos van descubriendo más y más cosas cada vez. Para Kuhn esto no es así. En vez de avance continuo hay una especie de sucesión de momentos de “stop and go”; en vez de evolución hay una secuencia de crisis y revoluciones sucesivas. En los momentos de estabilidad entre revoluciones, los científicos investigan bajo un conjunto de teorías y métodos completamente aceptados por la comunidad científica. A esto lo llama Kuhn hacer “ciencia normal” bajo un determinado “paradigma científico”. Mientras el paradigma se mantiene, la situación es estable. ¿Cuándo se derrumba el paradigma? De entrada podría pensarse: cuando aparecen situaciones en las cuales el paradigma falla. Cuando aparecen contraejemplos, casos en que no sucede lo que teoría predice. Pero Kuhn cree que esto no es así: un paradigma establecido tiene una gran capacidad para asimilar contraejemplos. Los científicos tienden a pensar que el contraejemplo quedará explicado con algún retoque superficial de la teoría, y se esfuerzan por buscar la manera de efectuar ese retoque. Y esto después de haber intentado desmontar el contraejemplo en base a errores de observación, de método, de instrumento, etc. Para que un paradigma se derrumbe hace falta, además, la existencia de un paradigma alternativo que solucione los contraejemplos, de la misma manera que para el derrumbamiento del “ancien regime” y el advenimiento de la Revolución Francesa hacía falta, además del descontento popular, la emergencia del paradigma de “Liberté, Fraternité, Egalité”.
El ejemplo favorito de Kuhn es la situación de la física a principios del siglo XX. Durante mucho tiempo la investigación bajo el paradigma newtoniano había permitido un gran desarrollo de dicho paradigma y una aplicación a ámbitos de problemas cada vez mayores, pero al mismo tiempo había provocado la aparición de numerosos contraejemplos. Tenía especial relevancia la desviación de la órbita de Mercurio: el planeta más próximo al sol no circulaba exactamente siguiendo las normas que Newton había establecido. El descubrimiento de esta anomalía no provocó el derrumbamiento de la física newtoniana, sino numerosos intentos de “parchearla”. Y cuando Einstein formuló su teoría de la relatividad, gracias a la cual Mercurio volvía a circular de acuerdo con las normas, esto tampoco supuso la aceptación instantánea del nuevo paradigma y el correspondiente rechazo del anterior. Durante un tiempo muchos de los científicos que se habían formado bajo el antiguo paradigma, que habían investigado de acuerdo con él y que lo habían enseñado a sus alumnos, lo defendieron con uñas y dientes. Pero al final cayó. En este caso no fue necesario que rodara ninguna cabeza, al menos en sentido literal, al contrario de lo que sucedió en la Revolución Francesa. Los científicos son gente pacífica.
Es tentador aplicar de manera automática el modelo explicativo de Kuhn a la situación actual de la física: los físicos teóricos siguen haciendo “ciencia normal” bajo los paradigmas relativista o cuántico porque no ha emergido un nuevo paradigma que los supere. Viven en una situación prerrevolucionaria, atisbando la crisis, a la espera de que aparezca alguien que enarbole un nuevo estandarte en el que puedan creer. Pero la revolución se hace esperar demasiado: los propios protagonistas de la revolución anterior ya eran conscientes de que quedaba algo por hacer, y cien años después seguimos igual. Con lo cual volvemos al principio.

Evolución versus revolución en matemáticas
Con respecto a la historia de las matemáticas, el modelo de Kuhn no es tan fácil de aplicar de manera automática. En física la revolución relativista anuló la física newtoniana, y hoy podríamos prescindir de ella por completo si no fuera porque a nuestra escala produce los mismos resultados mediante uno cálculos mucho más sencillos. Pero en cambio los teoremas de Tales o Pitágoras siguen tan vigentes hoy como hace dos mil quinientos años. No puede decirse que en matemáticas haya revoluciones, sino más bien evolución. Acumulación.
Desde mi punto de vista esta última apreciación es engañosa. La ventaja de la matemática sobre la física es que no tiene que contrastarse con la realidad, y esto le da una gran capacidad para “absorber” anomalías. Las explicaciones nuevas coexisten con las antiguas, aunque la combinación produzca una cierta sensación de incoherencia. Pero no hay que decidir entre una y otra, porque no hay un término de comparación que obligue a descartar la que peor encaje. Desarrollaré lo que quiero decir a base de unos cuantos ejemplos.
Empecemos con Pitágoras. Para demostrar su famoso teorema utilizaba métodos geométricos. En aquel momento la aritmética contaba con poco más que los números naturales y las operaciones básicas, y la notación numérica de los griegos y los romanos (los “números romanos”) hacían imposible un cálculo algebraico competente. Por tanto, para demostrar la equivalencia entre los cuadrados de los catetos y de la hipotenusa, dibujaba cuadrados sobre cada uno de los lados del triángulo rectángulo y luego demostraba geométricamente la equivalencia entre superficies. Pero por otra parte Pitágoras era un fanático de los números naturales. Fanático, sí, no exagero. Consideraba que los números eran la auténtica esencia de la realidad, porque son lo que le dan armonía y equilibrio. Pues bien: en algún momento algún pitagórico descubrió que si se intenta calcular la hipotenusa de un triángulo rectángulo cuyos catetos miden 1, no puede hacerse utilizando número enteros. La suma de los cuadrados de las catetos sería 1+1= 2, y por tanto lo hipotenusa sería la raíz cuadrada de 2. Pero este “número”, el resultado de calcular la raíz cuadrada de 2, no es un número natural, ni tampoco se puede expresar como una “relación” entre números naturales. Este descubrimiento abrió una crisis enorme en la escuela pitagórica, porque cuestionaba su metafísica y su mística numerológica, y también provocó una cierta crisis entre los matemáticos griegos.
Abrevio: la crisis de la matemática se cerró finalmente con la aceptación de los números irracionales. Igual que sucede en el caso de los números imaginarios, el nombre que se les dio indica que al principio fueron aceptados un poco a contrapelo. El adjetivo “irracional” aplicado al sustantivo “número” provoca un oxímoron: los números son la quintaesencia de la racionalidad. El caso es que al final se desarrolló la aritmética correspondiente, con sus operaciones y sus reglas, y quedaron plenamente integrados en el conjunto de los números. A diferencia de lo que sucede con la física, esta crisis no supuso una revolución que negara la validez del paradigma anterior.
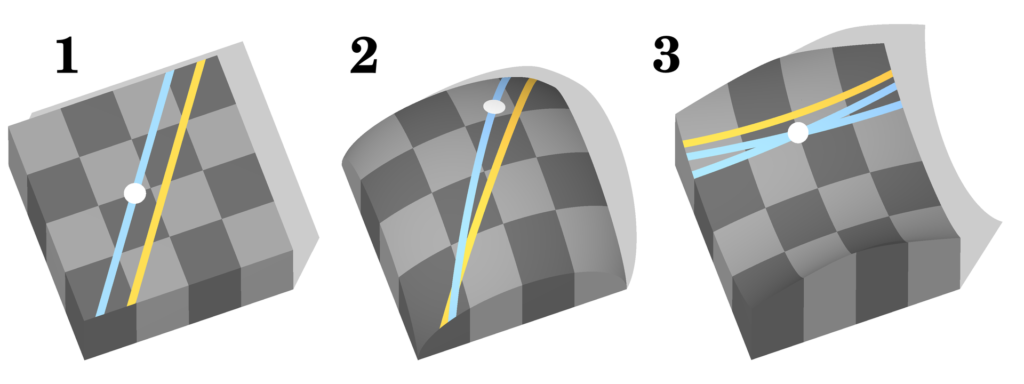
Una situación similar volvió a producirse en el siglo XIX con el intento de demostrar el quinto postulado de Euclides, el que dice que por un punto exterior a una recta solo puede trazarse una paralela. Al intentar demostrarlo por reducción al absurdo, diversos matemáticos comprobaron que no se llega a ninguna contradicción si se afirma que no puede trazarse ninguna, o que pueden trazarse infinitas. Obtuvieron simplemente geometrías en las que la superficie de dos dimensiones no es plana, sino más bien cóncava (geometría elíptica) o convexa (geometría hiperbólica). Si no hay contradicción no hay por qué elegir una y rechazar las demás. A diferencia con lo que sucede en la física, aquí no hay un término de comparación que obligue a considerar válido únicamente el modelo que mejor encaje con él.
Este último ejemplo es especialmente interesante para poner de manifiesto la diferencia que he mencionado entre la física y las matemáticas. Sucede que una de estas geometrías no-euclidianas, la hiperbólica, encaja perfectamente con la física relativista, por lo que los físicos consideran que la estructura geométrica del espacio es hiperbólica. Los matemáticos siguen a lo suyo, sin preocuparse por este detalle. Para ellos la geometría euclidiana es tan válida como las otras dos. No hay crisis, no se necesita una revolución que establezca un nuevo orden.
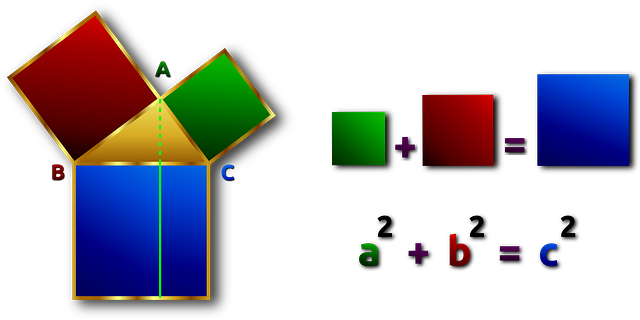
Esperando una razón revolucionaria
La física propone modelos que expliquen el comportamiento del mundo físico. En cada momento se considera válido el modelo que mejor encaja con lo que conocemos de ese mundo. En cambio la matemática tiene que encajar solo con la racionalidad: aquí todo es válido salvo lo que lleva a contradicción. En esto reside, tal vez, su grandeza y su miseria. Gracias a esta independencia de la realidad material, gracias a depender únicamente de la razón, la matemática es inmune a las revoluciones, y realiza plenamente el ideal platónico de verdades universales, necesarias y eternas. Nadie cuestionará nunca a Tales o a Pitágoras porque nadie podrá aportar nunca ningún contraejemplo, puesto que los contraejemplos aparentes, como podrían ser las geometrías no euclidianas, se aceptan al lado de los antiguos paradigmas. Al lado de ellos, no en lugar de ellos.
Pero tal vez esta grandeza de las matemáticas provoca a la vez su propia miseria, porque parece que sin revolución no hay progreso decisivo. En matemática sólo hay evolución, y la evolución amplía, pero no renueva. Tal vez la física actual solo podría avanzar si dispusiera de una matemática radicalmente diferente, con un punto de vista que suponga con respecto al anterior una ruptura del calibre de la que supuso la física de Newton con respecto a la de Aristóteles, o la de Einstein con respecto a la de Newton. Tal vez hiciera falta cuestionar el principio de no contradicción, aunque ahora mismo resulte imposible aceptar que pueda haber validez matemática, incluso validez lógica, si prescindimos de él. Pero también el principio de indeterminación de la mecánica cuántica parece contradecir los mismos fundamentos de la explicación científica y sin embargo los físicos lo han aceptado.
Un cuestionamiento tan radical de la matemática supondría, seguramente, un cuestionamiento similar de la lógica, esto es, de las reglas básicas de la razón. Parece imposible. De acuerdo en que tenemos el arte, que juguetea con las reglas de la razón, cuando no las ignora por completo, pero si lo que queremos es explicar la realidad y prever su comportamiento, parece imposible prescindir de dichas reglas.
He aquí una visión alternativa. Desprendámonos de la idea de que la razón capta la esencia de la realidad, de que lo real es racional y principios similares. Son antropomórficos: proyectan sobre lo que nos rodea nuestras propias actitudes. Veamos la razón como un instrumento del que nos ha dotado la evolución para maximizar nuestro éxito en la adaptación al medio. No hay más verdad en la razón que en el pulgar oponible o en la capacidad de fabricar instrumentos líticos. Que la razón haya sido un instrumento extraordinariamente eficaz significa solo eso, que ha sido una tirada de dados más afortunada que otras. Pero da de sí lo que da de sí, y tal vez llegue un punto en el que ya no de más de sí, o en el que tenga que evolucionar sustancialmente para dar más de sí.
La razón ha sido un instrumento tan eficaz de adaptación al medio que nos ha permitido modificar enormemente el propio medio. Y podemos preguntarnos si no podría ser que el medio en el que vivimos actualmente, tan diferente de aquel en el que se produjo el nacimiento de la razón, ya no sea tan favorable al uso de la propia razón. Por lo menos tal como la conocemos. Por supuesto que en los aspectos más básicos no ha cambiado nada: seguimos caminando y alimentándonos, y aquí podemos aplicar los reglas de siempre. Pero en los aspectos más nuevos y más alejados del medio inicial, el instrumento que surgió en él no tiene por qué ser apropiado. Por ejemplo, en física teórica. En lo muy, muy grande, y en lo muy, muy pequeño.
No puede negarse que cada nuevo avance del conocimiento supone una ruptura con verdades básicas que hasta entonces parecían irrebatibles. Y cada progreso decisivo hace que el medio en el que vivimos se aleje más del inicial, y esto es cierto tanto del medio propiamente dicho, el medio material, como de la comprensión que tenemos de él. La tierra bajo nuestros pies no es inmóvil, como se creyó durante tanto tiempo, aunque todas las apariencias nos hagan pensar que sí. El duro acero no es macizo, aunque lo parezca, sino que está formado por una enorme cantidad de partículas diminutas moviéndose a gran velocidad a través de un espacio básicamente vacío. El tiempo no transcurre de manera regular. El espacio no es plano. ¿No nos hemos alejado ya lo suficiente de los presupuestos básicos en los que descansaban las reglas básicas de la razón como para pensar que ha llegado el momento de cambiarlas?
Quizá sea necesaria una revolución que lleve a un nuevo paradigma en matemáticas. Es más: quizá sea necesaria una revolución que lleve a un nuevo paradigma racional. Quizá sea necesaria una nueva aproximación a lo real, una nueva mirada. Quizá algún día lleguemos a una visión de la realidad y del conocimiento en la que se unifiquen relatividad y mecánica cuántica, pero también mente y cerebro, inteligencia y pasión. Y puede que desde aquella nueva perspectiva la matemática actual y la lógica actual, incluyendo el principio de no contradicción, se vean como casos particulares de una explicación más amplia. Artificios útiles para movernos en el que ha sido nuestro medio hasta ahora, pero que dejan de ser válidos cuando se intentan utilizar a una escala más amplia.














